Figure 6 (page 13):
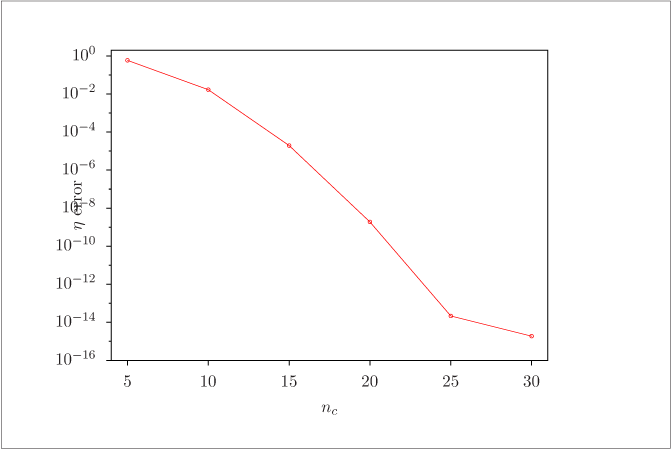
Relative error in the effectiveness factor versus number of collocation points.
Code for Figure 6
Text of the GNU GPL.
main.m
clear('all'); close('all');
% Copyright (C) 2001, James B. Rawlings and John G. Ekerdt
%
% This program is free software; you can redistribute it and/or
% modify it under the terms of the GNU General Public License as
% published by the Free Software Foundation; either version 2, or (at
% your option) any later version.
%
% This program is distributed in the hope that it will be useful, but
% WITHOUT ANY WARRANTY; without even the implied warranty of
% MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU
% General Public License for more details.
%
% You should have received a copy of the GNU General Public License
% along with this program; see the file COPYING. If not, write to
% the Free Software Foundation, 59 Temple Place - Suite 330, Boston,
% MA 02111-1307, USA.
global Phi A Aint Bint Rint n
Phi = 10;
n = 1;
nint = 100;
xint = linspace(0, 3, nint)';
colvec = [5; 10; 15; 20; 25; 30];
ncol = length(colvec);
etaan = 1./Phi*(1./tanh(3*Phi)-1/(3*Phi));
etaerror = zeros (ncol, 1);
for i = 1: ncol
npts = colvec(i);
%
% global collocation
%
[R A B Q] = colloc(npts-2, 'left', 'right');
R = R*3;
A = A/3;
B = B/9;
Q = Q*3;
Aint = A(2:npts-1,:);
Bint = B(2:npts-1,:);
Rint = R(2:npts-1);
%
% solve the problem
%
c0=0.5*linspace(0,1,npts)';
tol = 1e-10;
opts = optimset ('TolFun', tol, 'Display', 'off');
[c,fval,info] = fsolve('pellet',c0,opts);
%
% compute the effectiveness factor
%
eta = (n+1)/2*A(npts,:)*c/Phi^2;
etaerror(i) = abs(eta - etaan)/etaan;
end
table = [colvec etaerror];
save -ascii etaerr.dat table;
semilogy (table(:,1), table(:,2), '-o');
title ('Figure 6')
pellet.m
function retval = pellet(c)
global Phi A Aint Bint Rint n
npts = length(c);
cint = c(2:npts-1);
retval(1) = A(1,:)*c;
retval(2:npts-1,1) = Bint*c + 2*Aint*c./Rint - 2/(n+1)*Phi^2*(cint.^n);
retval(npts) = 1 - c(npts);
/export/home/jbraw/courses/cbe255/content/util/matlab/colloc.m
function [r, a, b, q] = colloc (n, varargin)
nargs = nargin;
if (nargs < 1 || nargs > 3)
error ('usage: [r, a, b, q] = colloc (n, ''left'', ''right'')');
end
if (~ (isnumeric (n) && numel (n) == 1 && round (n) == n))
error ('colloc: first argument must be an integer scalar');
end
if (isnan (n) || isinf (n))
error ('colloc: NaN is invalid as N');
end
if (n < 0)
error ('colloc: first argument must be non-negative');
end
n0 = 0;
n1 = 0;
for i = 2:nargs
s = varargin{i-1};
if (~ ischar (s))
error ('colloc: expecting character string argument');
end
s = lower (s);
if (strcmp (s, 'r') || strcmp (s, 'right'))
n1 = 1;
elseif (strcmp (s, 'l') || strcmp (s, 'left'))
n0 = 1;
else
error ('colloc: unrecognized argument');
end
end
nt = n + n0 + n1;
if (nt < 1)
error ('colloc: the total number of roots must be positive');
end
alpha = 0;
beta = 0;
%% Compute roots.
[dif1, dif2, dif3, r] = jcobi (n, n0, n1, alpha, beta);
%% First derivative weights.
a = zeros (nt, nt);
for i = 1:nt
a(i,:) = dfopr (n, n0, n1, i, 1, dif1, dif2, dif3, r)';
end
%% Second derivative weights.
b = zeros (nt, nt);
for i = 1:nt
b(i,:) = dfopr (n, n0, n1, i, 2, dif1, dif2, dif3, r)';
end
%% Gaussian quadrature weights.
id = 3;
q = dfopr (n, n0, n1, 0, id, dif1, dif2, dif3, r);
end
%% The following routines (JCOBI, DIF, DFOPR, INTRP, AND RADAU)
%% are the same as found in Villadsen, J. and M.L. Michelsen,
%% Solution of Differential Equation Models by Polynomial
%% Approximation, Prentice-Hall (1978) pages 418-420.
%%
%% Cosmetic changes (elimination of arithmetic IF statements, most
%% GO TO statements, and indentation of program blocks) made by:
%%
%% John W. Eaton
%% Department of Chemical Engineering
%% The University of Texas at Austin
%% Austin, Texas 78712
%%
%% June 6, 1987
%%
%% Some error checking additions also made on June 7, 1987
%%
%% Further cosmetic changes made August 20, 1987
%%
%% Translated from Fortran December 14, 2006
function vect = dfopr (n, n0, n1, i, id, dif1, dif2, dif3, root)
%% Villadsen and Michelsen, pages 133-134, 419
%%
%% Input parameters:
%%
%% N : The degree of the Jacobi polynomial, (i.e. the number
%% of interior interpolation points)
%%
%% N0 : Determines whether x = 0 is included as an
%% interpolation point
%%
%% n0 = 0 ==> x = 0 is not included
%% n0 = 1 ==> x = 0 is included
%%
%% N1 : Determines whether x = 1 is included as an
%% interpolation point
%%
%% n1 = 0 ==> x = 1 is not included
%% n1 = 1 ==> x = 1 is included
%%
%% I : The index of the node for which the weights are to be
%% calculated
%%
%% ID : Indicator
%%
%% id = 1 ==> first derivative weights are computed
%% id = 2 ==> second derivative weights are computed
%% id = 3 ==> Gaussian weights are computed (in this
%% case, I is not used).
%%
%% Output parameters:
%%
%% DIF1 : vector containing the first derivative
%% of the node polynomial at the zeros
%%
%% DIF2 : vector containing the second derivative
%% of the node polynomial at the zeros
%%
%% DIF3 : vector containing the third derivative
%% of the node polynomial at the zeros
%%
%% VECT : vector of computed weights
if (n0 ~= 0 && n0 ~= 1)
error ('dfopr: n0 not equal to 0 or 1');
end
if (n1 ~= 0 && n1 ~= 1)
error ('dfopr: n1 not equal to 0 or 1');
end
if (n < 0)
error ('dfopr: n less than 0');
end
nt = n + n0 + n1;
if (id ~= 1 && id ~= 2 && id ~= 3)
error ('dfopr: id not equal to 1, 2, or 3');
end
if (id ~= 3)
if (i < 1)
error ('dfopr: index less than zero');
end
if (i > nt)
error ('dfopr: index greater than number of interpolation points');
end
end
if (nt < 1)
error ('dfopr: number of interpolation points less than 1');
end
%% Evaluate discretization matrices and Gaussian quadrature
%% weights. Quadrature weights are normalized to sum to one.
vect = zeros (nt, 1);
if (id ~= 3)
for j = 1:nt
if (j == i)
if (id == 1)
vect(i) = dif2(i)/dif1(i)/2.0;
else
vect(i) = dif3(i)/dif1(i)/3.0;
end
else
y = root(i) - root(j);
vect(j) = dif1(i)/dif1(j)/y;
if (id == 2)
vect(j) = vect(j)*(dif2(i)/dif1(i) - 2.0/y);
end
end
end
else
y = 0.0;
for j = 1:nt
x = root(j);
ax = x*(1.0 - x);
if (n0 == 0)
ax = ax/x/x;
end
if (n1 == 0)
ax = ax/(1.0 - x)/(1.0 - x);
end
vect(j) = ax/dif1(j)^2;
y = y + vect(j);
end
vect = vect/y;
end
end
function [dif1, dif2, dif3, root] = jcobi (n, n0, n1, alpha, beta)
%% Villadsen and Michelsen, pages 131-132, 418
%%
%% This subroutine computes the zeros of the Jacobi polynomial
%%
%% (ALPHA,BETA)
%% P (X)
%% N
%%
%% Input parameters:
%%
%% N : The degree of the Jacobi polynomial, (i.e. the number
%% of interior interpolation points)
%%
%% N0 : Determines whether x = 0 is included as an
%% interpolation point
%%
%% N0 = 0 ==> x = 0 is not included
%% N0 = 1 ==> x = 0 is included
%%
%% N1 : Determines whether x = 1 is included as an
%% interpolation point
%%
%% N1 = 0 ==> x = 1 is not included
%% N1 = 1 ==> x = 1 is included
%%
%% ALPHA : The value of alpha in the description of the jacobi
%% polynomial
%%
%% BETA : The value of beta in the description of the Jacobi
%% polynomial
%%
%% For a more complete explanation of alpha and beta, see Villadsen
%% and Michelsen, pages 57 to 59
%%
%% Output parameters:
%%
%% ROOT : vector containing the n + n0 + n1 zeros of the node
%% polynomial used in the interpolation routine
%%
%% DIF1 : vector containing the first derivative
%% of the node polynomial at the zeros
%%
%% DIF2 : vector containing the second derivative
%% of the node polynomial at the zeros
%%
%% DIF3 : vector containing the third derivative
%% of the node polynomial at the zeros
if (n0 ~= 0 && n0 ~= 1)
error ('jcobi: n0 not equal to 0 or 1');
end
if (n1 ~= 0 && n1 ~= 1)
error ('jcobi: n1 not equal to 0 or 1');
end
if (n < 0)
error ('jcobi: n less than 0');
end
nt = n + n0 + n1;
if (nt < 1)
error ('jcobi: number of interpolation points less than 1');
end
dif1 = zeros (nt, 1);
dif2 = zeros (nt, 1);
dif3 = zeros (nt, 1);
root = zeros (nt, 1);
%% First evaluation of coefficients in recursion formulas.
%% recursion coefficients are stored in dif1 and dif2.
ab = alpha + beta;
ad = beta - alpha;
ap = beta*alpha;
dif1(1) = (ad/(ab + 2.0) + 1.0)/2.0;
dif2(1) = 0.0;
if (n >= 2)
for i = 2:n
z1 = i - 1.0;
z = ab + 2*z1;
dif1(i) = (ab*ad/z/(z + 2.0) + 1.0)/2.0;
if (i == 2)
dif2(i) = (ab + ap + z1)/z/z/(z + 1.0);
else
z = z*z;
y = z1*(ab + z1);
y = y*(ap + y);
dif2(i) = y/z/(z - 1.0);
end
end
end
%% Root determination by newton method with suppression of
%% previously determined roots.
x = 0.0;
for i = 1:n
done = false;
while (~ done)
xd = 0.0;
xn = 1.0;
xd1 = 0.0;
xn1 = 0.0;
for j = 1:n
xp = (dif1(j) - x)*xn - dif2(j)*xd;
xp1 = (dif1(j) - x)*xn1 - dif2(j)*xd1 - xn;
xd = xn;
xd1 = xn1;
xn = xp;
xn1 = xp1;
end
zc = 1.0;
z = xn/xn1;
if (i ~= 1)
for j = 2:i
zc = zc - z/(x - root(j-1));
end
end
z = z/zc;
x = x - z;
if (abs(z) <= 1.0e-09)
done = true;
end
end
root(i) = x;
x = x + 0.0001;
end
%% Add interpolation points at x = 0 and/or x = 1.
nt = n + n0 + n1;
if (n0 ~= 0)
for i = 1:n
j = n + 1 - i;
root(j+1) = root(j);
end
root(1) = 0.0;
end
if (n1 == 1)
root(nt) = 1.0;
end
%% Use recursion formulas to evaluate derivatives of node polynomial
%%
%% N0 (ALPHA,BETA) N1
%% P (X) = (X) * P (X) * (1 - X)
%% NT N
%%
%% at the interpolation points.
for i = 1:nt
x = root(i);
dif1(i) = 1.0;
dif2(i) = 0.0;
dif3(i) = 0.0;
for j = 1:nt
if (j ~= i)
y = x - root(j);
dif3(i) = y*dif3(i) + 3.0*dif2(i);
dif2(i) = y*dif2(i) + 2.0*dif1(i);
dif1(i) = y*dif1(i);
end
end
end
end
