Figure 2 (page 5):

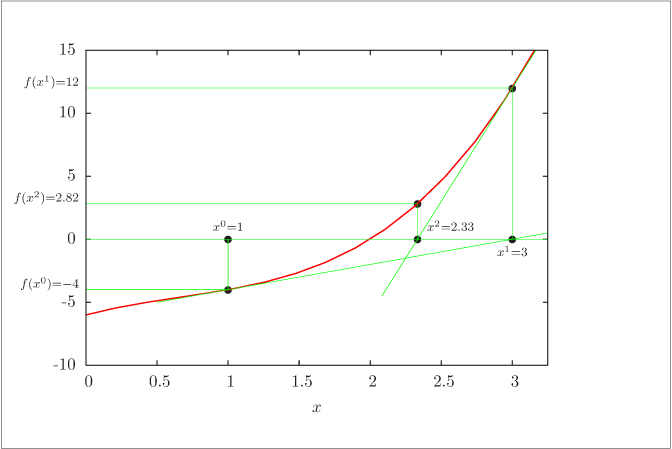
Two iterations of Newton's method for f(x) = x^3 - 2x^2 + 3x - 6 = 0.

Code for Figure 2

Text of the GNU GPL.

main.m

clear('all'); close('all');

npts = 20;
x = linspace(0, 4, npts)';


fx = f(x);

x0 = 1;
fx0 = f(x0);
dfx0 = df(x0);

x1 = x0 - fx0/dfx0;
fx1 = f(x1);
dfx1 = df(x1);

x2 = x1 - fx1/dfx1;
fx2 = f(x2);

gap = 0.5;
xzero = [0; 4];
yzero = [0; 0];
xt0 = [x0 - gap; x1 + gap];
yt0 = fx0 + dfx0 * (xt0-x0);
xt1 = [x1 + gap/2; x2 - gap/2];
yt1 = fx1 + dfx1 * (xt1-x1);

pts = [x0, 0,   x1, 0,   x2, 0;
       x0, fx0, x1, fx1, x2, fx2;
       0,  fx0, 0,  fx1, 0,  fx2];

tangents = [xzero, yzero, xt0, yt0, xt1, yt1];

plot(x, fx, pts(:,1), pts(:,2), pts(:,3), pts(:,4), ...
     pts(:,5), pts(:,6), xzero, yzero, xt0, yt0, xt1, yt1)

table1 = [x fx];

save newton_function.dat table1
save newton_points.dat pts
save newton_tangent.dat tangents

f.m

function retval = f(x)
  retval = x.^3 - 2*x.^2 + 3*x -6;

df.m

function retval = df(x)
  retval = 3*x.^2 -4*x + 3;